Math homework help -
adding and subtracting
mixed numbers
Students send me scans (or cell phone pictures) of their math homework with their own answers written down. I review and rectify mistakes, if any so that they have all correct answers by the time they turn them in to their school teachers. I also make efforts to explain the concepts/steps briefly.
Note that this is a paid service but
costs significantly less than live tutoring sessions. Here are a few
examples from pre algebra to show what I receive and what I send back. You can use these solutions as solved examples to learn on your own. Don't miss out on the tips and tricks, if any.
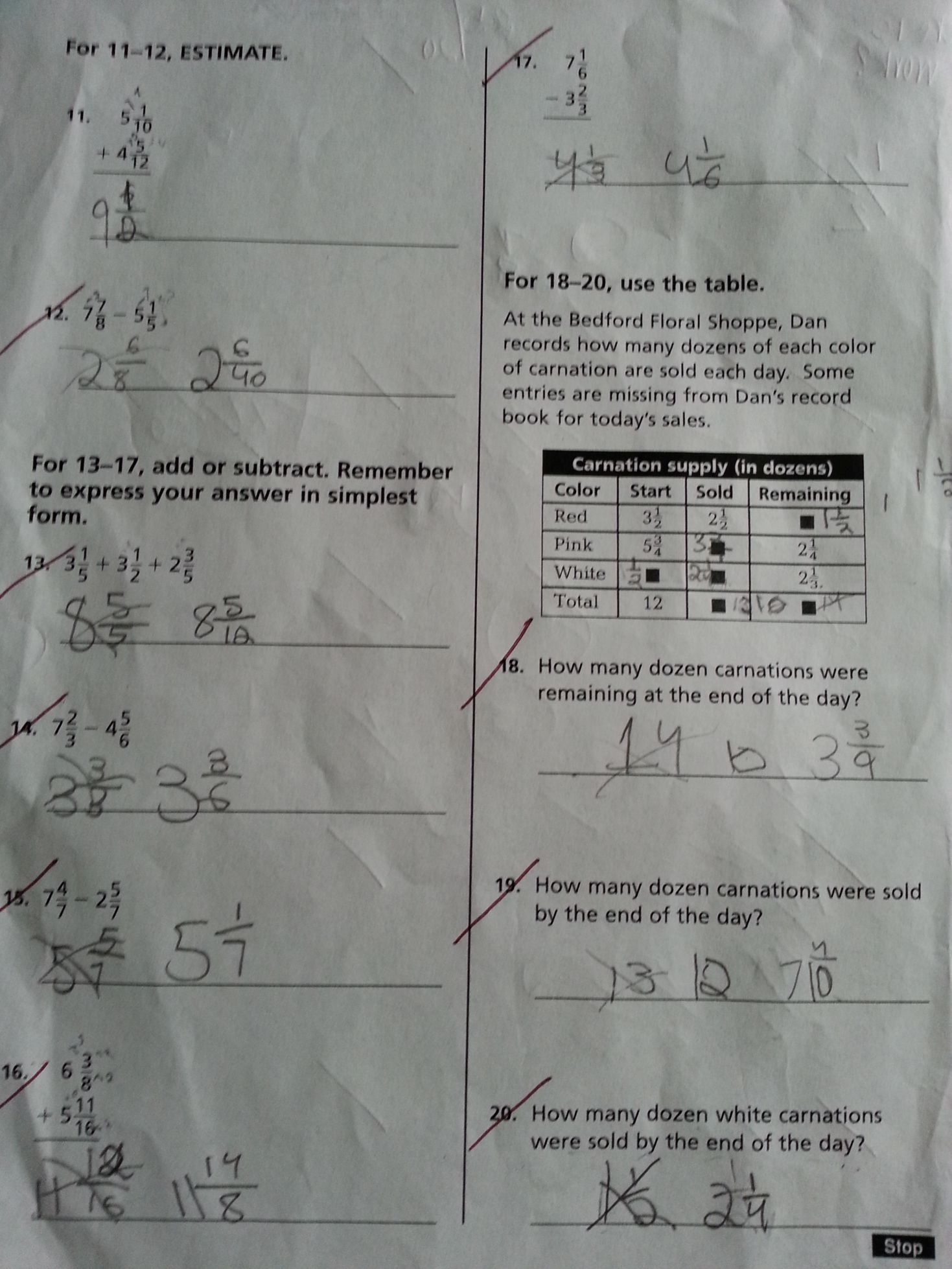
Add and subtract mixed numbers - 1
Add and subtract mixed numbers - 2
Add and subtract mixed numbers - 1

What I received |

What I sent back |
|
click on pictures to enlarge |
|
- The more common method of adding mixed numbers is to add the whole numbers together and add the fractions together. However, you can also convert each of the mixed numbers to improper fractions and add them up. If you do them this way, don't forget to convert your final answer (obtained as an improper fraction) back to a mixed number. After all, you want to write down your final answer as a mixed number when you are adding mixed numbers.
Take for example #2
5 3⁄4 + 6 5⁄12
= 23⁄4 + 77⁄12
= 69⁄12 + 77⁄12
= 146⁄12
= 12 2⁄12 that simplifies to 12 1⁄6
- Look at problem #5. One way of doing that is already shown in the picture. This could have been done in another way: subtract 2 from 8 so you get 6; 6 - 4⁄7; = 5 3⁄7;
More sample maths homework help by email
Add and subtract mixed numbers - 2
What I received |

What I sent back |
|
click on pictures to enlarge |
|
Look at #14 for example.
7 2⁄3 - 4 5⁄6
= 23⁄3 - 29⁄6
= 46⁄6 - 29⁄6
= 17⁄6
= 2 5⁄6
| Home | | | Live homework help | | | More sample email homework help |