Math homework help -
multiplying fractions
and mixed numbers
Students send me scans (or cell phone pictures) of their math homework with their own answers written down. I review and rectify mistakes, if any so that they have all correct answers by the time they turn them in to their school teachers. I also make efforts to explain the concepts/steps briefly.
Note that this is a paid service but costs significantly less than live tutoring sessions. Here are a few examples from pre algebra to show what I receive and what I send back. You can use these solutions as solved examples to learn on your own. Don't miss out on the tips and tricks, if any.
Multiplying fractions and mixed numbers 1
Multiplying fractions and mixed numbers 2
Multiplying fractions and mixed numbers 3
Multiplying fractions and mixed numbers 1

What I received |

What I sent back |
|
click on pictures to enlarge |
|
Multiplying fractions and mixed numbers 2
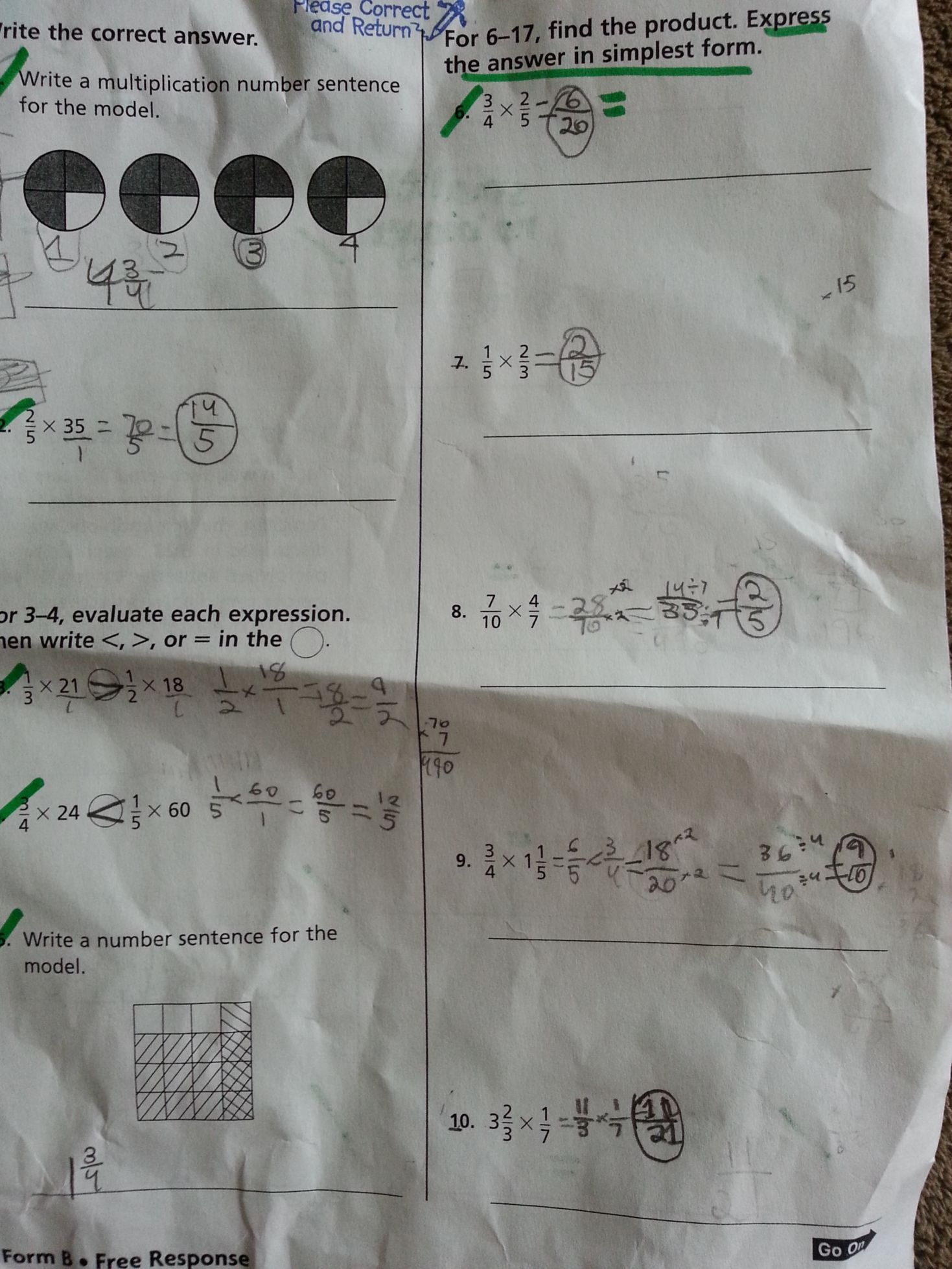
What I received |
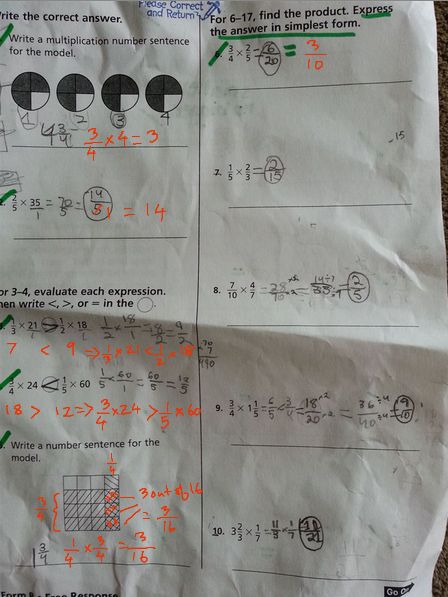
What I sent back |
|
click on pictures to enlarge |
|
Multiplying fractions and mixed numbers 3

What I received |

What I sent back |
|
click on pictures to enlarge |
|
More sample maths homework help
Take for example 7⁄9 × 45⁄28
If you follow the rule of fraction multiplication, you get
(7 × 45)⁄(9 × 28) (two multiplications, takes time)
= 315⁄252
Then you need to reduce 315⁄252 to it's lowest term, which means you need to find a number that can divide both 315 and 252 and keep dividing until you get the answer in the simplest form. The final answer is 5⁄4 = 1 1⁄4.
If you do it in this method, you don't do anything wrong but that's not the best way to do the multiplication. Multiplying and then dividing is as good as taking one step to the left and one step to the right which effectively means you come back to the same place. No doubt that takes time and therefore, is an inefficient way to multiply fractions.
Instead, use cross reduction first. Divide 7 from the numerator and 28 from the denominator by 7. That leaves 1 in place of 7 and 4 in place of 28.
Similarly, divide 45 from the numerator and 9 from the denominator with 9. That leaves 5 in place of 45 and 1 in place of 9.
7⁄9 × 45⁄28
=
= 5⁄4 = 1 1⁄4.
Don't you find this easier?
| Home | | | Live homework help | | | More sample email homework help |