Math tutoring online -
finding the angle between
the hands of a clock
when the time is...
By the time you finish reading this page and watching the video, you will be able to find the angle between the hour and minute hands of a clock at any given time.
What is the angle between the hour and minute hands of the clock when the time is...let's say anything?
Before
you want to try out the problem in the recorded lesson at the bottom of
this page, let's try a simpler version: find the angle between the hour
and minute hands of the clock when the time is 2:30 (am or pm doesn't really matter).
To answer
this question, most students get the first step right, which is to
remember that the angle around the whole circle is 360°. Therefore, the angle between the consecutive digits, say between 2 and 3 is, 360° ÷ 12 = 30°.
The mistake
It's in the next step that students tend to stumble, when they make an oversimplified assumption that the hour hand stays put at one number throughout the hour and jumps to the next number at the start of the next hour.
So to answer the question asked, many students would draw the following picture and come to the conclusion that the required angle between the two hands when the time is 2:30 is 120°.
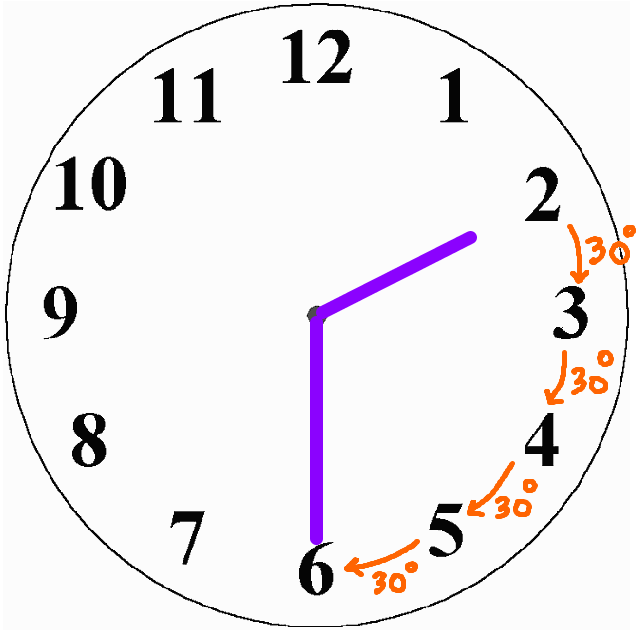
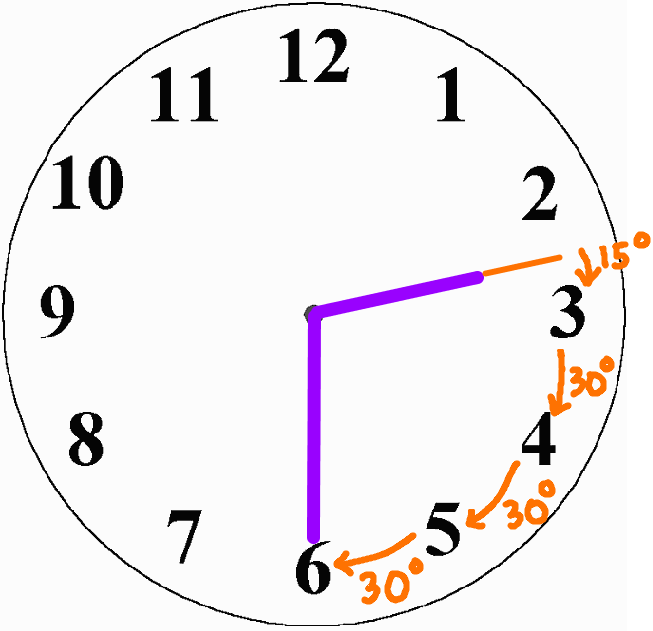
However, in reality, the hour hand/small hand of the clock keeps ticking throughout the hour. So, by the time the minute hand reaches 6 (half past two), the hour hand has moved exactly half way from 2 to 3. Therefore, the angle between the small hand and 3 is not 30° but half of that, or 15°. This is shown in the picture below.
Qualities to look for in an online math tutor
Thus, the angle between the two hands at 2:30 is 15° + 30° + 30° + 30° = 105°.
You could actually extend this idea to find the angle between the hands of the clock at any given time. Watch out the following video and see if it makes sense.
Angle between the hour and minutes hands of the clock at 1:50
Recorded online math tutoring sessions
Got it? It's the fraction into the hour (30 minutes = 1⁄2, 50 minutes = 5⁄6, and so on) that you should take into consideration to determine the angle between the small hand and the next hour. Your turn
a) Find the larger angle between the hour and minute hands of the clock when the time is 10:20
(Ans: 190 °)
b) Find the smaller angle between the hour and minute hands of the clock when the time is 4:45
(Ans: 127.5 °)
| Home | | | Online tutoring | | | Homework help |