Online Math tutoring -
piecewise functions
By the time you finish reading this page and watching the videos, you will understand how to graph and solve problems related to piecewise functions.
When you see the equation of a function and nothing has been mentioned about its domain (that is, the values of x for which the function is defined), you make an assumption that the function is defined for its entire domain. The graph of the function follows the same equation throughout.
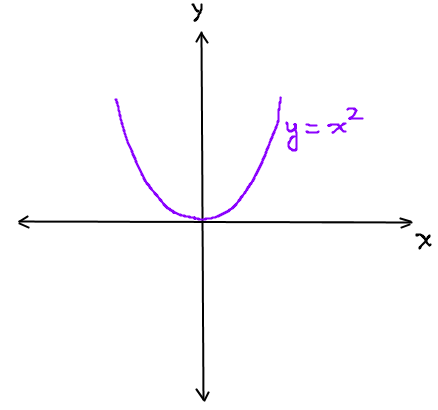
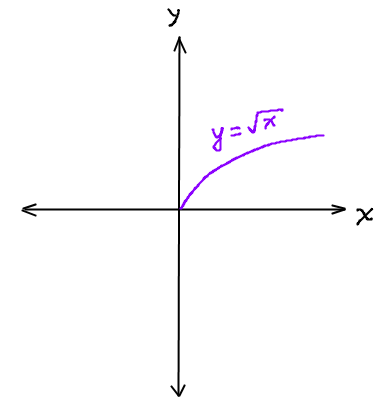
In a piecewise function, the graph follows different equations for different values of x. For example, the graph could be a straight line when x is negative and an exponential function when x is zero or more.
The overall graph is the combination of graphs of different functions for different stretches of the independent variable (x).
Watch the following recorded session to understand how to draw such functions on a graph paper. By the way, can you think of a common piecewise function we often talk about? Watch on.
Piecewise defined functions
Indeed, the absolute value function is a great example of piecewise functions. However, piecewise functions don't have to follow any pattern or look symmetrical like the absolute value function does.
Consider the example in the video below. I encourage you to pause the video once the equations are written down, and try drawing the graph on your own.
A real life example of piecewise functions
Here comes a real life example of piecewise functions. The problem in the following video has been closely modeled around example 9, section 2.2 from the book "Precalculus - Graphing and Data Analysis" (Prentice Hall).
Looking for a math tutor online? Here are some things to check out.
Like the student in the video, I'd expect most students to get part (a) right. Many might get part (b) right as well. However, only a few would usually get part (c) right in the first attempt.
| Home | | | Online tutoring | | | Homework help |