SAT Math strategy -
use suitable numbers for variables
in Algebra

Complete list of SAT Math tips and strategies is here

For high school students, Algebra is often the most dreaded areas in Math. The reason is its abstract nature - you are asked to do Math operations on 'numbers' that are not known to you.

Algebra is an integral part of the SAT. I strongly recommend that you brush up the basics of Algebra and do adequate practice before you take on the test. From experience, I know this is easier said than done (well, at least for some students). The examples on this page will show you how to score points on certain type of Algebra problems even without knowing how to do them using Algebra. Let's begin.

Solution 1: Let's spend some time learning how to solve this using Algebra. That's because the Algebra solution to this problem requires that you apply several important skills. Skills that you cannot afford to overlook in your overall SAT prep. Here comes the more 'traditional' solution.

1. How to factor a difference of two squares
2. How to take common factors out from an Algebraic expression
3. How to write one variable in terms of another
4. How to combine like terms

Click here for more SAT Math tips and techniques

Solution 2: Okay, so you dread Algebra but would still love to score a point on this problem. The next video shows how to do that.

Doing this way was no doubt easier but when you solve problems by using numbers in place of variables, pay extra attention to the nature of the numbers - for this problem they had to be positive and consecutive even and q had to be the larger of the two.

Here's one more.

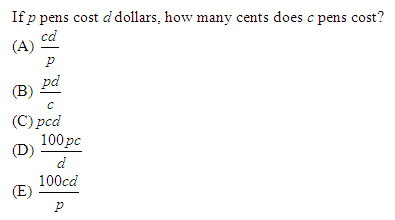
Solution 1: For this problem, using Algebra (or shall I say using pure logic?) will be quicker. Let's first do it that way.

That was more of logic, right? Okay, now here comes the alternative solution, the one without Algebra.

Solution 2: Pick some easy, small numbers for the variables in the problem. Replace the variables with those numbers and check which option will give you the right numerical answer if the variables were to actually represent those numbers. Watch on.

Although the method above was good enough to take us to the right option, note that in the worst case (when option (E) is the correct answer) you would need to check options (A) through (D) to find out which one fits the bill.

A final word of caution: if you are solving a problem using this method, avoid using 0 or 1 for any of the variables. The reasons are obvious, think!

Click here for more SAT Math tips, strategies and best practices