SAT Math help

Watch the following video related to SAT Math. And then, watch how I'd prefer to solve the same problem (if I were to be a student not great with my Algebra skills).

The problems below have been taken from the "Official SAT Study Guide" from the College Board

Problem: A restaurant has 19 tables that can seat a total of 84 people. Some of the tables seat 4 people and the others seat 5 people. How many tables seat 5 people?
(A) 4
(B) 5
(C) 6
(D) 7
(E) 8

Solution 1:

The solution above is technically perfect. That's exactly how you want to solve such a problem when presented in your school exam, without any option.

However, not all test takers are so good in Algebra that they could frame and solve the two equations in x and y and be able to do that in about a minute (you only get about a minute to read and then solve a Math problem on the SAT).

Now watch the video below to see how you could have scored on this problem even without knowing how to solve multi-variable equations in one minute.

Solution 2:

NOTE: The idea of showing the two videos is not to compare my teaching ability with the other person but to make you aware, through a live example, that SAT demands that you think outside the box. Did you notice how starting at option (C) helped me get to the right answer in the minimum number of steps?

Watch me do live SAT tutoring here. But don't forget to come back to review the next example on this page.

Here comes another example. Once again, the first solution (Solution 1) is from a very popular Math videos website. My way of solving follows next (Solution 2).

Problem:

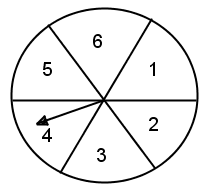
On the disk shown above, a player spins the arrow twice. The fraction ^a⁄_b is formed, where a is the number of the sector where the arrow stops after the first spin and b is the number of the sector where the arrow stops after the second spin. On every spin, each of the numbered sectors has an equal probability of being the sector on which the arrow stops. What is the probability that the fraction ^a⁄_b is greater than 1?
(A) ¹⁵⁄₃₆
(B) ¹⁶⁄₃₆
(C) ¹⁸⁄₃₆
(D) ²⁰⁄₃₆
(E) ²¹⁄₃₆

Solution 1:

Once again, prefect solution, as you would expect from a Math expert. However, it still makes me wonder how many high school students could do all of that in about a minute? Let me see if we could apply some logic and reduce the number of steps (and save some of the scarce resource called 'time'!).

Solution 2:

As you could see, after we eliminated those six cases where the number on the first spin was the same as the number on the second spin (a = b so that ^a⁄_b is neither greater than nor less than but exactly equal to 1), we just had to use some logic to figure out that the remaining 30 cases would be evenly divided into the two possible scenarios (a > b and a < b).

After you have reviewed the basic concepts on SAT Math, you should try to master techniques like the ones shown above - ones that help you maximize your score and save you time.

Click here to watch a sample SAT Math lesson

More SAT Math tips and techniques (click on each link below)

Make a construction
Use numbers for variables