SAT Math tip -
make a construction on given figure

Complete list of SAT Math tips and strategies is here

Some Math problems on the SAT come with figures. Often, life becomes a lot easier if you can make a small construction on the given figure.

By making a construction I mean drawing something more than what's already given - often a straight line joining two given points or a straight line parallel to another line and so on. You are allowed to write and draw on your test booklet and you should take full advantage of this provision.

The following examples will give you an idea on the nature of problems you could apply this technique on and how best to do it.

Solution: You must be wondering it's got to do with that smaller angle on the other side of x. Angle around a full circle is 360° and therefore x is 360 minus that angle. Right approach. To find that angle though, is a bit of a challenge if you stick to the exact same figure without any plan to modify it.

Video below shows how a small construction could earn you a point on this problem.

So you got the idea, haven't you? Let's use another example.

The problem below has been taken from the "Official SAT Study Guide" from the College Board

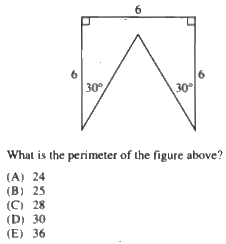
Solution:"This is easy...I know how to find the perimeter...just add up the side lengths...(pause)...wait...the figure has 5 sides but they gave us only 3...perimeter is 6 + 6 + 6 + something + something...I need to find out the two slanted sides" is probably what you said to yourself.

The options do not help because all of them are larger than 18 (therefore elimination does not work). So what do you do? Just draw a line and you are done (well, almost). Watch on.

Completing the triangle made all the difference, right? Okay, one more...

The problem below has been taken from the "Official SAT Study Guide" from the College Board

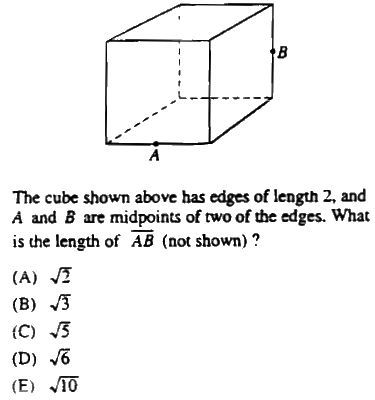
Solution:The one thing special about this problem is that it is in 3-D. The line from A to B is not in the plane of paper.

But one thing's for sure. The length from A to B is surely more than the length of an edge of the cube and therefore the answer is larger than 2. A quick check with your calculator reveals that options (A) and (B) may be immediately ruled out. If you have to guess, pick one from (C), (D) and (E).

With a small construction (other than joining A and B with a straight line segment!), though, you can actually solve the problem. Let's see how.

Other than knowing which line to draw there were at least a couple of takeaways from this problem.

1. On the SAT, do not be tempted to use your calculator on every problem. Smart test takers would always look at the options first before deciding whether to use calculator or not.
2. If you come to get an equation involving the square of an unknown it does not mean you always have to take the square root to find the value of the unknown. Look ahead. The next step decides if you actually need to find the value of the unknown or if the square itself is what you need.

Click here for more SAT Math practice questions, tips and strategies